-
ראיתי לא מזמן חידה בתכנות שאהבתי, וחשבתי לשתף כאן את החברים:
נוסח החידה הוא פחות או יותר כך:בהנתן פונקציה המייצרת מספרים אקראיים (לצורך העניין, בין 0 ל 1 ), עליך להעריך בקירוב את הערך של הקבוע π (פאי).
במבט ראשון זה נראה כמו בדיחה, אבל באמת קיים פתרון חביב בכמה שורות של קוד.
הערה:
גוגל נותן מיד את הפתרון, אז לאמיצים עדיף להתאפק מלהציץ שם... במקום זה, למי שרוצה הנה רמז:
הנוסחה לחישוב שטח מעגל היא πr² (פאי כפול ריבוע הרדיוס של המעגל) -
ראיתי לא מזמן חידה בתכנות שאהבתי, וחשבתי לשתף כאן את החברים:
נוסח החידה הוא פחות או יותר כך:בהנתן פונקציה המייצרת מספרים אקראיים (לצורך העניין, בין 0 ל 1 ), עליך להעריך בקירוב את הערך של הקבוע π (פאי).
במבט ראשון זה נראה כמו בדיחה, אבל באמת קיים פתרון חביב בכמה שורות של קוד.
הערה:
גוגל נותן מיד את הפתרון, אז לאמיצים עדיף להתאפק מלהציץ שם... במקום זה, למי שרוצה הנה רמז:
הנוסחה לחישוב שטח מעגל היא πr² (פאי כפול ריבוע הרדיוס של המעגל) -
@odeddvir אני אמיץ ולא מסתכל בגוגל... אבל לא הבנתי את השאלה. מספרים אקראיים הם אקראיים וקבוע פאי הוא קבוע, מה הקשר בינהם? מה הכוונה להעריך?
-
@odeddvir אני אמיץ ולא מסתכל בגוגל... אבל לא הבנתי את השאלה. מספרים אקראיים הם אקראיים וקבוע פאי הוא קבוע, מה הקשר בינהם? מה הכוונה להעריך?
-
@רחמים אמר:
מה הכוונה להעריך?
לתת הערכה של הקבוע π עם דיוק מספק, למשל את 4 הספרות אחרי הנקודה העשרונית.
-
@odeddvir תחלק את ההיקף ברוחב ותקבל דיוק עם כמה מספרים שאתה רוצה לא רק 4. מה קשור כאן מספרים אקראיים?
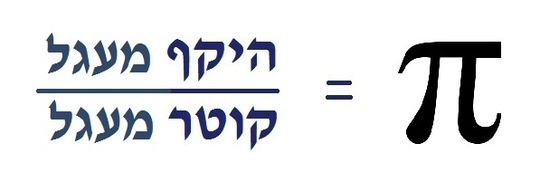
-
@odeddvir
לא קשור לתיכנות אבל זה הרעיון...טכניקה לא שגרתית לחישובו היא "שיטת מונטה קרלו": על לוח עץ נצייר ריבוע שאורך צלעו שתי יחידות. נצייר מעגל חסום בריבוע זה (זהו מעגל שרדיוסו שווה ליחידה אחת), ונתחיל להטיל חיצים אל הריבוע (לא נכוון את החץ למרכז הריבוע, אלא אל הריבוע כולו, באופן אקראי). לאחר מספר רב של הטלות, היחס, בין מספר הפעמים שהחצים פגעו בתוך המעגל למספר הפעמים שבהם פגעו בתוך הריבוע, שואף ליחס שבין שטחי שתי הצורות.
-
@odeddvir
לא קשור לתיכנות אבל זה הרעיון...טכניקה לא שגרתית לחישובו היא "שיטת מונטה קרלו": על לוח עץ נצייר ריבוע שאורך צלעו שתי יחידות. נצייר מעגל חסום בריבוע זה (זהו מעגל שרדיוסו שווה ליחידה אחת), ונתחיל להטיל חיצים אל הריבוע (לא נכוון את החץ למרכז הריבוע, אלא אל הריבוע כולו, באופן אקראי). לאחר מספר רב של הטלות, היחס, בין מספר הפעמים שהחצים פגעו בתוך המעגל למספר הפעמים שבהם פגעו בתוך הריבוע, שואף ליחס שבין שטחי שתי הצורות.
@רחמים כאשר מדובר על תוכנה ולא על לוח עץ פיזי, עדיין חסר פה שלב. איך נחשבן איזה מהמספרים האקראיים נמצא בתוך העיגול ואיזה מחוצה לו?
(כנראה צריך קצת טריגונומטריה... מתמטיקה הוא לא מהצדדים החזקים שלי...
אולי משהו כזה, נגיד שנדמיין ריבוע של מאה פיקסלים על מאה פיקסלים. סה"כ 10000 פיקסלים. נקח מספר אקראי בין 0-1 ונכפיל אותו ב-10000 כדי לקבל מיקום בריבוע. עכשיו נחשבן אם המיקום בתוך העיגול או מחוצה לה. וזאת על ידי שנחשב את המרחק שלו מהנקודה האמצעית של העיגול. נגיד שקיבלנו את המספר 3455. נחלק ב-100 כדי לקבל את השורה שבו הוא נמצא ונקח את השארית כדי לקבל את העמודה. יוצא שהוא בשורה 34 עמודה 55. המרכז של הריבוע נמצא בין שורה 50 לשורה 51 בגובה ובין עמודה 50 ל-51 ברוחב. בחישוב קל נמצא שהמיקום שקיבלנו גבוה מהרכז ב16 פיקסלים ומשוך לצד ימין ב-5 פיקסלים. כדי לקבל את המרחק מהמרכז נשרטט בדמיוננו משולש שהצד השוכב שלו הוא ברוחב 5 וצד העומד בגובה 16 ונשתמש בחשבון פיתאגרוס כדי לקבל את האלכסון שיוצא משהו כמו 16.76. טוב, מספר נמוך מ-50 אומר שהמיקום בתוך העיגול. ככל שנמשיך על זו הדרך ונחשבן את היחס של המספרים שבתוך העיגול למספרים שמחוצה לו נגיע יותר קרוב למספר PI) -
-
@רחמים כאשר מדובר על תוכנה ולא על לוח עץ פיזי, עדיין חסר פה שלב. איך נחשבן איזה מהמספרים האקראיים נמצא בתוך העיגול ואיזה מחוצה לו?
(כנראה צריך קצת טריגונומטריה... מתמטיקה הוא לא מהצדדים החזקים שלי...
אולי משהו כזה, נגיד שנדמיין ריבוע של מאה פיקסלים על מאה פיקסלים. סה"כ 10000 פיקסלים. נקח מספר אקראי בין 0-1 ונכפיל אותו ב-10000 כדי לקבל מיקום בריבוע. עכשיו נחשבן אם המיקום בתוך העיגול או מחוצה לה. וזאת על ידי שנחשב את המרחק שלו מהנקודה האמצעית של העיגול. נגיד שקיבלנו את המספר 3455. נחלק ב-100 כדי לקבל את השורה שבו הוא נמצא ונקח את השארית כדי לקבל את העמודה. יוצא שהוא בשורה 34 עמודה 55. המרכז של הריבוע נמצא בין שורה 50 לשורה 51 בגובה ובין עמודה 50 ל-51 ברוחב. בחישוב קל נמצא שהמיקום שקיבלנו גבוה מהרכז ב16 פיקסלים ומשוך לצד ימין ב-5 פיקסלים. כדי לקבל את המרחק מהמרכז נשרטט בדמיוננו משולש שהצד השוכב שלו הוא ברוחב 5 וצד העומד בגובה 16 ונשתמש בחשבון פיתאגרוס כדי לקבל את האלכסון שיוצא משהו כמו 16.76. טוב, מספר נמוך מ-50 אומר שהמיקום בתוך העיגול. ככל שנמשיך על זו הדרך ונחשבן את היחס של המספרים שבתוך העיגול למספרים שמחוצה לו נגיע יותר קרוב למספר PI)@yossiz אמר בחידה חביבה: כיצד להעריך בקירוב את הקבוע π באמצעות מספרים אקראיים:
כנראה צריך קצת טריגונומטריה
כל פונקציה מתמטית שתגלה לך אם אתה בתוך העיגול - מבוססת על הפאי, ואיך אתה יכול להשתמש בפונקציה זו כאשר אתה בא לברר מהו הפאי, אתה עדיין לא יודע מהו הפאי!
-
@yossiz אמר בחידה חביבה: כיצד להעריך בקירוב את הקבוע π באמצעות מספרים אקראיים:
כנראה צריך קצת טריגונומטריה
כל פונקציה מתמטית שתגלה לך אם אתה בתוך העיגול - מבוססת על הפאי, ואיך אתה יכול להשתמש בפונקציה זו כאשר אתה בא לברר מהו הפאי, אתה עדיין לא יודע מהו הפאי!
-
@yossiz אז למה לך להגריל מספרים אקראיים, פשוט תעבור על כל הפיקסלים ותספור כמה מהם בתוך העיגול וכמה בחוץ וככה תדע את הפאי - לפי היחס שבינהם?
-
@yossiz אז למה לך להגריל מספרים אקראיים, פשוט תעבור על כל הפיקסלים ותספור כמה מהם בתוך העיגול וכמה בחוץ וככה תדע את הפאי - לפי היחס שבינהם?
-
@רחמים אתה צודק. אני מקווה שהפתרון הסופי מאפשר להגיע לדיוק אינסופי - דבר שאי אפשר אם אתה ממיר את הריבוע לפיקסלים.
-
@רחמים זו דרך לא רעה, אבל הדיוק שלה מוגבל לרזולוציה של הריבוע. המספרים האקראיים הם כדי לשפר את הדרך הזו.
-
@odeddvir המספרים האקראיים למעשה מצביעים על פיקסלים, כך שגם הם בסופו של דבר תלויים ברזולוציה.
אגב, רזולוציה גבוהה היא לא בעיה כלל. קח ריבוע של 2 מליון על 2 מליון פיקסלים, ועיגול ברדיוס של 1 מליון, ויצא לך פאי עם 6 ספרות אחרי הנקודה.@רחמים השיטה שהבאת תעבוד, והדיוק המתקבל ממנה אכן תלוי ישירות ברוחב הריבוע (אם כי אני לא בטוח שהדיוק של 6 ספרות אחר הנקודה, זהה לסדר הגודל של הריבוע (מיליון ~ 6 ספרות בערך...)
החיסרון שלה לעומת הפתרון שאליו אני חותר, הוא סדר הגודל של החישובים הנדרשים (מליון*מליון=טריליון ).
). -
@רחמים השיטה שהבאת תעבוד, והדיוק המתקבל ממנה אכן תלוי ישירות ברוחב הריבוע (אם כי אני לא בטוח שהדיוק של 6 ספרות אחר הנקודה, זהה לסדר הגודל של הריבוע (מיליון ~ 6 ספרות בערך...)
החיסרון שלה לעומת הפתרון שאליו אני חותר, הוא סדר הגודל של החישובים הנדרשים (מליון*מליון=טריליון ).
).



 )
)