תרגיל מתמטי של הסתרת מזהה רץ

[קומפיונט]

טוב, @dovid אני רוצה לחשוף את כל הקלפים.
עשיתי פה קונץ קטן, אנא קבל את התנצלותי "...ומודה ועוזב ירוחם".

הפתרון שהצגתי הוא לא רעיון שלי (ודאי שלא, לא היתה הו"א בכלל) הוא פתרון שכיום נמצא בשימוש נרחב בתעשייה העולמית, ואפשר למצוא אותו כמעט בכל פינה. הפרוטוקולים המאובטחים של האינטרנט מבוססים עליו, והוא המלך של ההצפנות הא-סימטריות - הלא הוא ה-RSA!

אז כאמור, קבל את התנצלויותי על כך שלא חשפתי את הפרט הזה. חששתי להשתמש בנגזרת של צ.פ.נ. מפני שהבקשה הייתה מפורשת לא להשתמש בהצפנה אלא בתרגיל. ניסיתי להציע את זה בהתחלה (מבלי לצרף דוגמא), אבל אז חטפתי על הראש שלא קראתי היטב את השאלה. לכן בחרתי להציג את זה כתרגיל מתמטי ולא כהצפנה.

מה, וכי אני אשם שה-RSA משתמש בתרגיל המתמטי הפשוט הזה?!

@dovid נדמה לי שעכשיו אתה לא צריך הוכחות על הביטחון של התרגיל הזה.

[קומפיונט]

אני רוצה להוסיף עוד משהו קטן.

עכשיו קראתי בויקיפדיה על ה-RSA והתבאר לי משהו שלא היו מובן לי עד עכשיו.
אם אני מצפין באמצעות התרגיל שהצגתי (שהוא כאמור RSA) את הספרה 1 אז גם זה הפלט המוצפן (משום שהכפלה של 1 תמיד תחזיר 1) אז יש פה איזה חולשה.

קראתי שם על עוד כמה חולשות, לדוג' שאם הפורץ שולח קלט קצר והוא מקבל את התוכן המוצפן אז יתכן שהוא יוכל לפרוץ את זה בקלות (הבעיה המרכזית בנושא הזה).

אז הפתרון לבעיות האלו (שמשתמשים בו היום) הוא להשתמש עם ריפוד, ובעצם כבר הזכירו את זה פה @חגי ו @nigun שאפשר להשתמש עם מספרים רנדומליים שיטשטשו את המבנה של המספר המקורי.

אז המסקנה שלי שבשביל ערפול (או הצפנה) מוצלח צריך את שני הדברים הללו (התרגיל עצמו וטשטוש המבנה של ההודעה המקורית), וכל אחד בפני עצמו לא יהיה מספיק טוב.

אפשר לקרוא על זה פה תחת התת כותרת "ריפוד".

[dovid]

@קומפיונט זה לא הקונץ הראשון שלך... ואתה לא חושף הכל וגם לא כ"כ עוזב. אתה מרגיש שתכלס אתה רוכב על הסוס הנכון ומה זה משנה אם קצת הסתרת אי אלו פרטים לדרכי דיפלומטיה עקב דיון שנשמע כמו התקפה. אבל ככה אי אפשר לדון.
אני אדם שמאוד מכבד שכל, ונכנע לחלוטין לפני מי שמלמד אותי או מסביר לי או עוזר להבנה אצלי של משהו. אבל לא סיפקת לי מאלו כלום.
אני גם יכול לגבב בלי להבין מתודות מתורות ההצפנה ולחשוב שהם פשרה בין ביצועים לאבטחה, מבחינתי אני מהמהר ויכול להיות שאני מפסיד משני הצדדים.

בא נחזור לדיון בפסים שלך. אתה הצלחת לפרוץ את הרעיון המקורי עם כח גס שלקח כמה הנחות בחשבון (כ"הימור"). אז הנה קוד שפורץ את הרעיון שלך על אותו דרך, למזלך עשיתי אותו במחשב שלי.
הסריקה שעשיתי היא מטופשת לחולטין (מאוד יכול להיות שאפשר להקטין את הסריקה בהרבה עם כמה תרגילים מתמטיים), והיא מניחה כמה הנחות מקלות מאוד (אני צועד בדרכך), וזה אכן עדיין קשה למחשב: 41 שניות של כלל המעבדים שלי:

var numsEncrypted = new[] { 42993, 630, 40082, 9071, 54161, 15738, 51342, 25721, 52199, 49738, 50927, 13700, 37966, 3174, 35345 };

var primes =
    from n in Enumerable.Range(128, 512).AsParallel()
    where Enumerable.Range(2, (int)Math.Sqrt(n)).All(i => n % i > 0)
    select n;

var arr = primes.ToArray();
var allN = arr.SelectMany(a => arr.Select(x => x * a)).Distinct();


var st = Stopwatch.StartNew();
var keyD = allN.SelectMany(n => Enumerable.Range(1, 1000).Select(d => (n, d))).AsParallel().Where(e => TestNumber(e.d, e.n)).First();
st.Stop();
Console.WriteLine(st.Elapsed);
Console.WriteLine($"key founded: N: {keyD.n}, D: {keyD.d}");

foreach (var e in numsEncrypted)
    Console.WriteLine(BigInteger.Pow(e, keyD.d) % keyD.n);




bool TestNumber(int d, int n)
{
    var prev = BigInteger.Pow(numsEncrypted[0], d) % n;
    if (prev > 10000)
        return false;

    for (var o = 1; o < numsEncrypted.Length; o++)
    {
        var temp = BigInteger.Pow(numsEncrypted[o], d) % n;
        if (temp > 10000 || (temp - prev) != 1)
            return false;

        prev = temp;
    }

    return true;
}

[קומפיונט]

@dovid אני אוהב לעזור לכל מי שמבקש, התחום שאני חזק בו זה #C ו WPF, ובינתיים לא נתקלתי בבקשת עזרה בתחום הזה. אם אני יתקל בבקשת עזרה בתחום הזה, אהיה בל"נ הראשון שיעזור.

רוב השאלות שראיתי פה בפורום הם בנושא VBA או WinForm שאני לא מומחה בהם, בלשון המעטה.

עכשיו לגבי הקוד שפורץ את הרעיון, אני חושב שאני לא צריך להסביר לך שזה בגלל שהמפתחות שהקוד שהכנתי מייצר הם מפתחות קטנים, ולכן קל לשחזר אותם. אני בחרתי לייצר מספרים קטנים רק בגלל שיקולים של ביצועים.

קח לדוגמא את הספרות האלו:
1194494
719311
1944435
1477276
874876
1765046
1615810
1097120
1085181
1495561
1968819
1743848
171395
217310
1476345

אני משוכנע שזה כמעט לא אפשרי לשחזר את המפתח המקורי שלהם, (אולי זה ייקח כמה שנים...) וזה בגלל שעכשיו בחרתי למפתחות מספרים די גבוהים.

[dovid]

@קומפיונט כתב בתרגיל מתמטי של הסתרת מזהה רץ:

אני משוכנע שזה כמעט לא אפשרי לשחזר את המפתח המקורי שלהם, (אולי זה ייקח כמה שנים...) וזה בגלל שעכשיו בחרתי למפתחות מספרים די גבוהים.

בהחלט יכול להיות יקירי,
לא כדאי שלשם שלמות ההשוואה תבדוק קודם כמה שעות לוקח לבדוק את השיטה שלי בלי לדעת בכלל איזה איזור מספר אוחזים?
השיקול שלך לקחת מפתחות נמוכים לשם הביצועים עומד בסיס שאלתי ובבסיס השיטה שבחרתי. בינתיים השיטה הראשונה שמצאתי נראית לי עמידה (המספרים במקרה שלי בפרודקשיין אינם באיזור ה0-1500 כלל, אלא הרחק הרחק משם).

[mekev]

@mekev

אנקדוטה מעניינת לסיום השרשור

תראו איך האלגוריתם של גוגל פיענח את התוכן

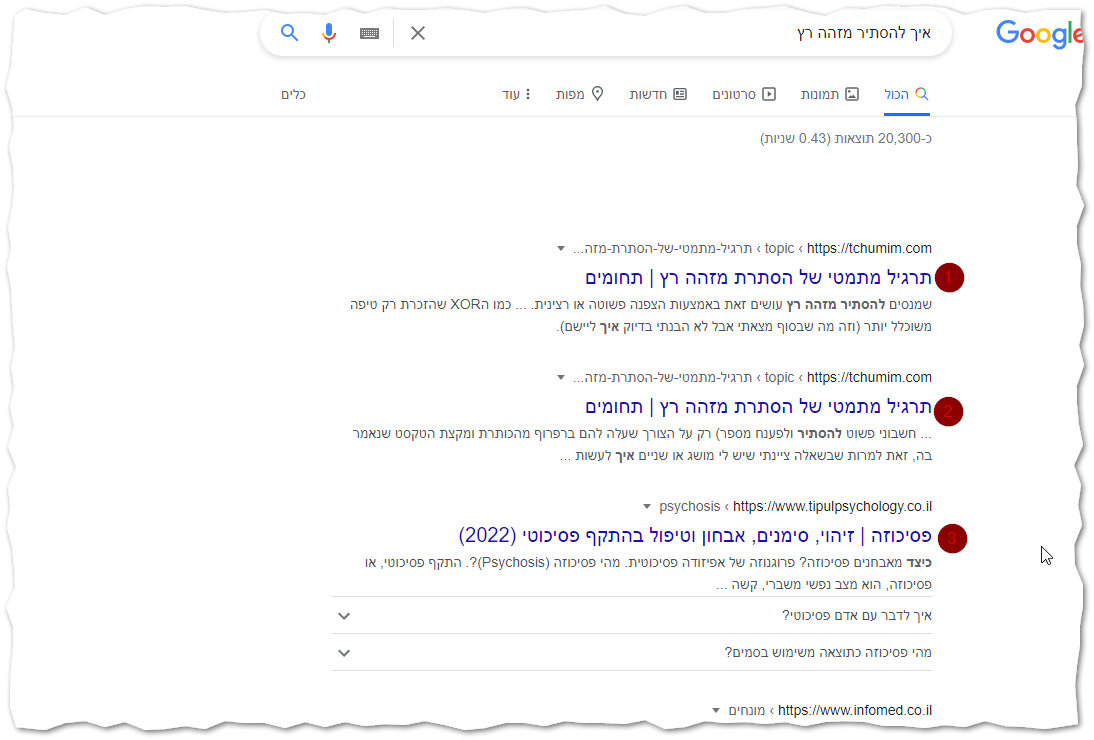
נ.ב. אין באמור כדי ח"ו לפגוע או לרמוז משהו על מישהו
נשלח כפרט משעשע שקפץ לי תוך כדי חיפוש פתרונות נוספים לשאלה

[yossiz]

@mekev יהיה באמת מעניין להבין מה גרם לגוגל לבחור באתר הזה, זה נראה התקף פסיכוטי של גוגל

בכל מקרה זה מראה כמה אי אפשר להגיע לתוצאות בחיפוש בעברית. זה היה מאוד מפתיע אותי אם היית מגיע למשהו טוב באמצעות חיפוש בעברית

[איש נחמד]

@yossiz כתב בתרגיל מתמטי של הסתרת מזהה רץ:

@mekev יהיה באמת מעניין להבין מה גרם לגוגל לבחור באתר הזה, זה נראה התקף פסיכוטי של גוגל

בכל מקרה זה מראה כמה אי אפשר להגיע לתוצאות בחיפוש בעברית. זה היה מאוד מפתיע אותי אם היית מגיע למשהו טוב באמצעות חיפוש בעברית

פשוט מאוד - אם תקרא את המילים המודגשות תראה שגוגל בחרה עבורו את צירוף המילים שהוא חיפש מתוך הצירוף הכי קרוב שלהם באשכול.
חיפוש של הסתרת מזהה רץ יראה ככה: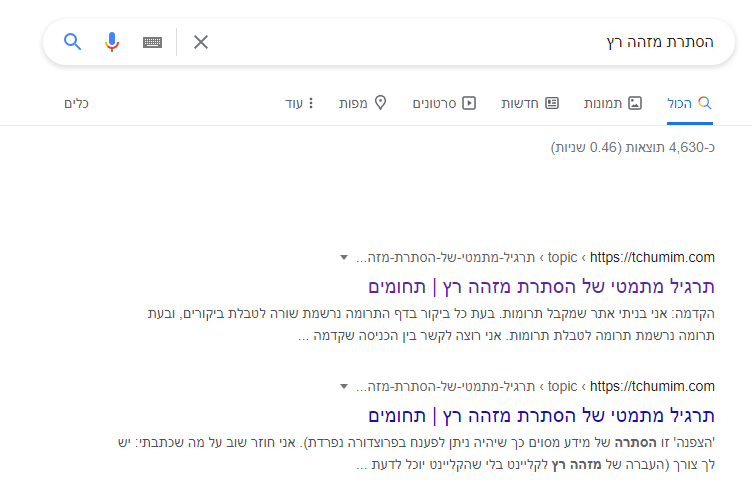

וזה :

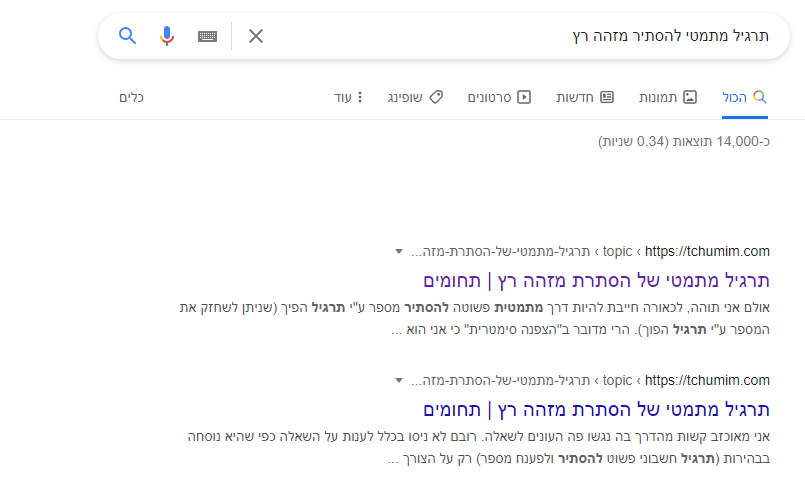
התוצאה השנייה שחוזרת על עצמה בהרבה מההטיות היא פשוט... הפוסט עם הכי הרבה לייקים בשרשור...

[קומפיונט]

פוסט זה נמחק!

[dovid]

@קומפיונט חבל על טרחתך.
אם היית רוצה שבאמת אדון בדבריך או אלמד ממך או אלמד אותך,
קמצוץ של דרך ארץ וכבוד אלי יחד עם כנות והוגנות, וכולנו היינו מרויחים.
לקחת את ההערה שלי ש"לשם שלמות ההשוואה תבדוק קודם כמה שעות לוקח לבדוק את השיטה שלי" ועשית לה מניפולציה עלובה כדי להמשיך לקנטר.
חבל, וצר לי על מאמציך שהפונו לספורט שלילי.
זו תגובה אחרונה שלי, בה הרשיתי לעצמי "להציל" את כבודי שמגיע לי ביושר רב.

[קומפיונט]

@dovid לא ציפיתי לכזו תגובה חריפה
נכון שעשיתי 'קונצים' בעבר, אבל אולי חזרתי בתשובה?
אני מבחינתי פותח דף חדש.