פענוח היסטוגרמה
-
אני רוצה להבדיל בין סוגי תמונות.
בין תמונה מצולמת לתמונה למצויירת.
עכשיו אם אני עושה הסטוגרמה. ( מדידה משוקללת של הסכום הכולל של ערכי הצבע ) אני מקבל הבדל ברור.
בגלל שבתמונה מצולמת יש הרבה יותר מגוון של צבעים.
כמו פה
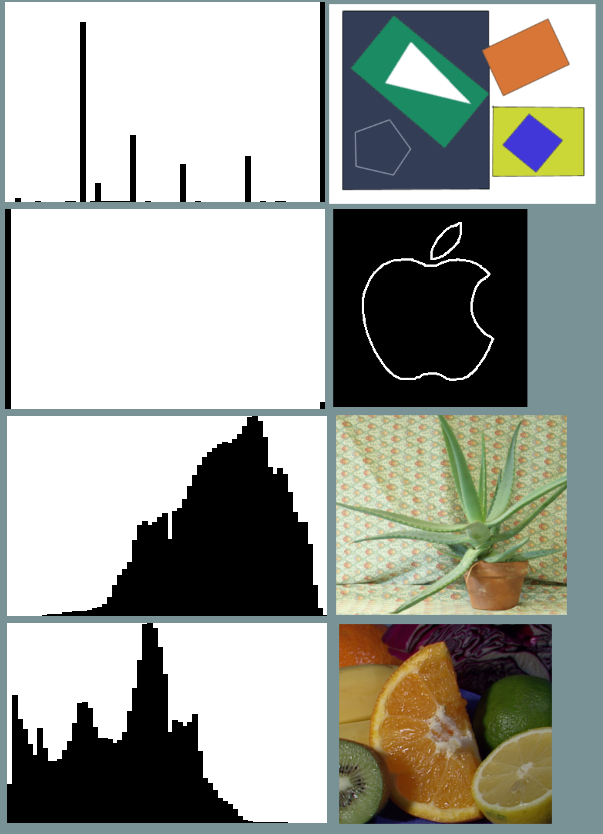
עכשיו אני מקבל את זה בצורת מערך של 64 אברים שכל אבר מכיל ערך לדוגמא מ 0 עד 1. כל אבר מיצג בתמונה קו ואם הוא 100 הקו מופיע עד למעלה ואם הוא 0 הוא לא מופיע בכלל ואם הוא 0.5 הוא מופיע חצי וכן הלאה.
איך אני יכול לקבוע כלל שיהיה אפשר לפי המערך להבדיל בין תמונה מצולמת לתמונה מצויירת.
פורסם במקור בפורום CODE613 ב17/07/2013 23:36 (+03:00)
-
אתה מתכוון בין תמונה מצולמת לבין שירטוט/איור ממוחשב, כי ציור מעשה ידי אדם, כשהוא סרוק, יכול גם הוא להיות עשיר בגוונים כגון צבעי גואש וכדומה.
אז אני הייתי עושה אלגוריתם שמבחין בין צבעים קרובים, כלומר ככל שיש יותר גיוון בדרגות קירוב באותו צבע, זה יותר נוטה סטטיסטית לתמונה מצולמת, קח לדוגמא את התפוז, יש בו כל כך הרבה גוונים של כתום, שלא ייתכן לומר שזה איור. כשמאיירים תפוז, הייתי מצפה לכל היותר ל 4-5 גווני כתום.
בהצלחה.
פורסם במקור בפורום CODE613 ב17/07/2013 23:53 (+03:00)
-
איזה מאתגר הנושא

אני מתמקד בשאלתך ולא בהקדמה:
לפי מה שאני רואה בדוגמאות, אז הרעיון הוא סטיית תקן גבוהה (מעל 0.2 נגיד).
אולי בשביל ביצועים עדיף לבדוק סטיית תקן מדגמית.הנה דוגמא מאקסל, שתי טורים, הימיני כאילו ציור והשמאלי תמונה:
0.80 0.20
0.00 0.25
0.00 0.30
0.30 0.35
0.00 0.40
0.00 0.35
0.40 0.30
0.00 0.25
0.00 0.20
0.00 0.15התוצאה של הנוסחה STDEV.P (סטיית התקן מלאה לא מדגמית)
0.257875939 לטור הימני.
0.075 לטור השמאלי.פורסם במקור בפורום CODE613 ב18/07/2013 11:15 (+03:00)
-
עכשיו אני מקבל את זה בצורת מערך של 64 אברים שכל אבר מכיל ערך לדוגמא מ 0 עד 1. כל אבר מיצג בתמונה קו ואם הוא 100 הקו מופיע עד למעלה ואם הוא 0 הוא לא מופיע בכלל ואם הוא 0.5 הוא מופיע חצי וכן הלאה.
איך אני יכול לקבוע כלל שיהיה אפשר לפי המערך להבדיל בין תמונה מצולמת לתמונה מצויירת.
חשב את הממוצע של כל האברים במערך אם הממוצע מעל 50 בוודאי שזה מצולם ואם פחות מ 10 בוודאי שזה ציור.
וכמובן ממוצע זה חיבור של כל האיברים לחלק במספר האיברים.פורסם במקור בפורום CODE613 ב18/07/2013 16:40 (+03:00)
-
עכשיו אני מקבל את זה בצורת מערך של 64 אברים שכל אבר מכיל ערך לדוגמא מ 0 עד 1. כל אבר מיצג בתמונה קו ואם הוא 100 הקו מופיע עד למעלה ואם הוא 0 הוא לא מופיע בכלל ואם הוא 0.5 הוא מופיע חצי וכן הלאה.
איך אני יכול לקבוע כלל שיהיה אפשר לפי המערך להבדיל בין תמונה מצולמת לתמונה מצויירת.
חשב את הממוצע של כל האברים במערך אם הממוצע מעל 50 בוודאי שזה מצולם ואם פחות מ 10 בוודאי שזה ציור.
וכמובן ממוצע זה חיבור של כל האיברים לחלק במספר האיברים.שים לב, ממוצע בכל מקרה מיותר לחשב, כי ממוצע נדרש רק כשמס' האיברים משתנה, פה הוא קבוע (64) ומספיק סיכום.
שנית, אני לא הייתי בטוח שאמנם ישנה חוקיות שההיסטוגרמה של תמונה תכיל יותר בס"ה, אבל זה במת מה שקורה בדוגמאות שהוא הביא.פורסם במקור בפורום CODE613 ב21/07/2013 12:18 (+03:00)
-
הנה ניתוח חדש:
לפי מה שאני הבנתי היסטוגרמה היא מבנה של קוים עומדים 64 במספר, כל קו עומד הוא כנגד צבע אחר, גובה הקו נקבע ע''פ כמות של אותו צבע בתמונה כולה ולכן בתמונה של השחור לבן ראינו את הקו הראשון שמיצג את הצבע שחור גבוה עד למעלה כיון שיש הרבה צבע שחור בתמונה, וכל שאר הקווים הם על 0 כיון שאין צבעים אחרים כלל, והקו האחרן הוא קטן כיון שהוא מיצג את הצבע הלבן ואותו יש מעט.
עוד נתון: ההבדל בין תמונה לצילום הוא שבצילום יש הרבה צבעים שונים ותמונה לא, אבל מבחינת כמות עבור כל צבע אין הבדל ברור בין צילום לתמונה.
א''כ המסקנה העולה היא שכדי להבדיל בין תמונה לצילום צריך לעבור על המערך ולבדוק כמה צבעים נמצאים על כמות אפס, אם הם רבים הרי שאין הרבה צבעים שונים וזו תמונה אם אין כמעט איברים במערך שערכם 0 הרי שזה צילום, ואין צורך להתיחס לאורך הקו אלא רק אם הוא גדול מ0 או לא.אבל עדיין לא נראה שזה יתן תוצאות נכונות בכל מקרה, לדעתי כדי להבדיל בין תמונה לצילום לא תועיל היסטוגרמה אלא צריך לעבור כל כל הפיקסילים או על כמות מדגמית ולראות כמה פעמים הצבע משתנה מפיקסיל לפיקסיל, כלומר האם רוב הפעמים פיקסיל נתון שווה בצבעו לפיקסיל השכן, או שרוב הפעמים פקסילים שכנים שונים זה מזה בצבעם.
פורסם במקור בפורום CODE613 ב21/07/2013 12:31 (+03:00)
-
הרעיון של ספירת האפסים לכאורה נכון ומהיר יותר מהרעיונות האחרים.
מה שכתבת
@רחמיםאלא צריך לעבור כל כל הפיקסילים או על כמות מדגמית ולראות כמה פעמים הצבע משתנה מפיקסיל לפיקסיל, כלומר האם רוב הפעמים פיקסיל נתון שווה בצבעו לפיקסיל השכן, או שרוב הפעמים פקסילים שכנים שונים זה מזה בצבעם.
זה לא בדיוק מה שהצעתי לעיל?
פורסם במקור בפורום CODE613 ב21/07/2013 13:58 (+03:00)
-
את האמת שאני לא הסברתי על ההיסטוגרמה.
היא בנויה מהאפור לבן שבן שנוצר מהצבעוני.
אחרי שזה אפור לבן יש ערוץ אחד של צבע מ 0 עד 255 שזה סכום כולל של 256
256/64 = 4.
שזה אומר שהוא מונה את כל הכמות של הפיקסלים שיש לכל צבע בתמונה.ולפי זה הוא מיצר את הגרף.
אם זה 64 קוים אז הוא מצרף קבוצות קבוצות של 4 נגיד 256 255 254 253 יהיו קו אחד. זה בשביל לא לרדת לקטנות.
למען האמת הוא מקצץ את ההיסטוגרמה מלמעלה ומלמטה. עד איפה שמתחילים להיות שינויים.
לכן אפשר לראות קו שמלא עד למעלה ואחרי זה מלא קוים קטנים שזה אל כל ההיטוגרמה בשלמותה. כי כל הקווים ביחד אמורים ליצור את הקו הכי ארוך בחשבון אלא שהוא חותך את התצוגה. למינימום ומקסימום.
פורסם במקור בפורום CODE613 ב21/07/2013 15:40 (+03:00)
-
@דוד ל.ט.
איזה מאתגר הנושא

אני מתמקד בשאלתך ולא בהקדמה:
לפי מה שאני רואה בדוגמאות, אז הרעיון הוא סטיית תקן גבוהה (מעל 0.2 נגיד).
אולי בשביל ביצועים עדיף לבדוק סטיית תקן מדגמית.הנה דוגמא מאקסל, שתי טורים, הימיני כאילו ציור והשמאלי תמונה:
0.80 0.20
0.00 0.25
0.00 0.30
0.30 0.35
0.00 0.40
0.00 0.35
0.40 0.30
0.00 0.25
0.00 0.20
0.00 0.15התוצאה של הנוסחה STDEV.P (סטיית התקן מלאה לא מדגמית)
0.257875939 לטור הימני.
0.075 לטור השמאלי.בגלל שאני מתכנת ב js אז מצאתי את זה.
http://jsfiddle.net/hiddenloop/TPeJt/
שעושה את אותו ביצוע כנראה.
פורסם במקור בפורום CODE613 ב25/07/2013 21:43 (+03:00)
